Hemingroth

Genetically evolved perfect Tic-Tac-Toe player

Introduction

Tic-Tac-Toe, a simple yet engaging game, has entertained individuals for centuries [1]. Its origins can be traced back to ancient Egypt, with variations appearing across diverse cultures. Fundamentally, the game involves two players alternating turns, aiming to form a straight line of three of their respective symbols on a 3x3 grid. A key characteristic of Tic-Tac-Toe is its deterministic nature: with optimal play, neither player can guarantee a win, resulting in a draw. The limited number of possible game states renders it amenable to exhaustive analysis and the development of optimal strategies via computational algorithms. Genetic algorithms, inspired by biological evolution, have proven effective in solving complex optimization problems. These algorithms operate on a population of candidate solutions, iteratively improving them through processes analogous to natural selection. Given the discrete and constrained search space of Tic-Tac-Toe, a genetic algorithm is well-suited to evolve an optimal playing strategy, efficiently navigating the game's state space to identify a solution that avoids losing [2].

Search space

The total number of possible Tic-Tac-Toe board configurations is 3^9, accounting for each cell having three possible states (X, O, or blank). However, many of these configurations are invalid, as they represent states where a player has already won in a previous turn. Furthermore, due to the inherent symmetry of the 3x3 grid, each valid configuration has seven equivalent counterparts achievable through rotations and reflections. By identifying and eliminating invalid and symmetrical states, we can significantly reduce the search space [3].

Figure 1: The 8 geometric variants for every unique game scenario [3].

A recursive, exhaustive search was employed to generate all unique, valid game scenarios, revealing 627 such scenarios. This reduced search space represents the complete set of possible game states that the genetic algorithm will explore.


enum Cell {
  O = -1,
  Empty = 0,
  X = 1,
}
type Scenario = Array&lt;Cell&gt;;

function variants(
  s: Scenario,
): Map<Scenario, (s: Scenario) => Scenario> {
  return new Map([
    [identity(s), (s) => identity(s)],
    [rotate(s), (s) => rotate(rotate(rotate(s)))],
    [rotate(rotate(s)), (s) => rotate(rotate(s))],
    [rotate(rotate(rotate(s))), (s) => rotate(s)],
    [flip(s), (s) => flip(s)],
    [rotate(flip(s)), (s) => flip(rotate(rotate(rotate(s))))],
    [rotate(rotate(flip(s))), (s) => flip(rotate(rotate(s)))],
    [rotate(rotate(rotate(flip(s)))), (s) => flip(rotate(s))],
  ]);
}

function base(s: Array&lt;Scenario&gt;): Scenario {
  return s.sort()[0];
}

function toKey(s: Scenario): number {
  return s.reduce((acc, v) => acc * 10 + (v + 2), 0);
}

Figure 2: Sample code demonstrating how a game scenario is reduced to its base case, before being encoded as an integer to act as a key in the hashmap that represents a candidate solution genome.

Training

Each candidate solution within the genetic algorithm's population is represented as an array of integers. The array's keys correspond to each unique game scenario identified in the search space. The values associated with each key are integers between 0 and 8, representing the cell to be played in that specific scenario. An initial population of *n* candidate solutions is generated, with array values randomly initialized. Each candidate solution's fitness is evaluated by playing it against every possible game variation. The scoring mechanism rewards solutions that result in wins or draws, while penalizing losses [3]. After evaluating the fitness of all candidate solutions, the most fit individuals are selected to form the next generation. These selected solutions undergo genetic operations: crossover, replication, and mutation. Crossover combines the genetic material of two parent solutions to create offspring; replication duplicates successful solutions; and mutation introduces random changes to individual solutions, promoting diversity. This iterative process continues until a candidate solution achieves a perfect fitness score of 1, indicating it has not lost a single game during its evaluation.

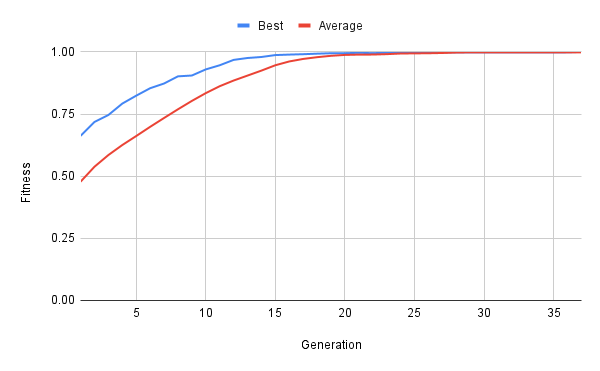
An optimal solution was found after 37 generations (~15 mins on a MacBook Air with Apple M2 chip and 8 GB memory) when running the training algorithm with the hyperparameters in Figure 3.


Population size = 2000
Sample size when picking genomes to populate next generation = 10
Probability of applying genetic operators:
  Mutation = 0.05
  Replication = 0.05
  Crossover = 0.1

Figure 3: Hyperparameters used during training.


time=18s,gen=1,best=0.66215,avg=0.47777
time=37s,gen=2,best=0.71820,avg=0.53799
time=56s,gen=3,best=0.74614,avg=0.58505
time=75s,gen=4,best=0.79210,avg=0.62535
time=94s,gen=5,best=0.82392,avg=0.66154
time=118s,gen=6,best=0.85389,avg=0.69851
time=137s,gen=7,best=0.87284,avg=0.73415
time=157s,gen=8,best=0.90171,avg=0.76912
time=180s,gen=9,best=0.90503,avg=0.80285
time=202s,gen=10,best=0.92964,avg=0.83417
time=227s,gen=11,best=0.94628,avg=0.86201
time=247s,gen=12,best=0.96790,avg=0.88482
time=268s,gen=13,best=0.97552,avg=0.90480
time=290s,gen=14,best=0.97959,avg=0.92482
time=313s,gen=15,best=0.98730,avg=0.94634
time=336s,gen=16,best=0.98924,avg=0.96162
time=359s,gen=17,best=0.99080,avg=0.97174
time=385s,gen=18,best=0.99293,avg=0.97880
time=406s,gen=19,best=0.99467,avg=0.98435
time=433s,gen=20,best=0.99481,avg=0.98791
time=456s,gen=21,best=0.99635,avg=0.98917
time=483s,gen=22,best=0.99500,avg=0.98938
time=507s,gen=23,best=0.99657,avg=0.99103
time=536s,gen=24,best=0.99830,avg=0.99351
time=560s,gen=25,best=0.99833,avg=0.99416
time=585s,gen=26,best=0.99834,avg=0.99466
time=613s,gen=27,best=0.99837,avg=0.99571
time=637s,gen=28,best=0.99838,avg=0.99749
time=665s,gen=29,best=0.99838,avg=0.99820
time=691s,gen=30,best=0.99839,avg=0.99828
time=720s,gen=31,best=0.99839,avg=0.99831
time=745s,gen=32,best=0.99839,avg=0.99831
time=775s,gen=33,best=0.99839,avg=0.99832
time=800s,gen=34,best=0.99839,avg=0.99837
time=828s,gen=35,best=0.99839,avg=0.99834
time=858s,gen=36,best=0.99841,avg=0.99839
time=884s,gen=37,best=1.00000,avg=0.99832

Figure 4: Sample of output logs during training.

Figure 5: Training progression towards optimal solution, showing both best and average fitness in the population for each generation.

Conclusion

Genetic algorithms excel at solving optimization problems with large, complex search spaces, particularly those where the objective function is difficult to define or has multiple local optima. They are less effective for problems requiring precise analytical solutions or those with very small, well-defined search spaces. Their strength lies in their ability to explore and exploit the search space through an iterative, stochastic process, mimicking the evolutionary mechanisms of natural selection. The inspiration for genetic algorithms comes directly from the natural world, a domain that has historically provided a wealth of innovative ideas and solutions for human endeavors. The inherent robustness and adaptability of genetic algorithms, derived from evolutionary principles, make them a valuable tool for tackling a wide range of computational challenges, including the optimization of game-playing strategies as demonstrated in this project.

References

[1]

Tic-tac-toe. (n.d.). In Wikipedia. Retrieved January 6, 2025, from https://en.wikipedia.org/w/index.php?title=Tic-tac-toe&oldid=1266833508

[2]

Genetic algorithm. (n.d.). In Wikipedia. Retrieved December 28, 2024, from https://en.wikipedia.org/w/index.php?title=Genetic_algorithm&oldid=1265724203

[3]

Gregor Hochmuth. (2003). On the Genetic Evolution of a Perfect Tic-Tac-Toe Strategy. http://www0.cs.ucl.ac.uk/staff/ucacbbl/ftp/papers/koza/sp2003/hochmuth.pdf